Date & Time: Monday, August 31, 2009, 15:30-16:30.
Venue: Committee Room
Title: Ideals of Analytic Deviation One and Test Modules
Speaker: Ganesh Kadu, IIT Bombay
Abstract: Let R be a Cohen-Macaulay local ring of dimension d and M be a maximal Cohen-Macaulay R-module. Let I be an ideal of analytic deviation one and analytic spread d. We study the function
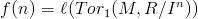whenever this length is finite. We give two natural conditions when this length becomes finite. The function f(n) is given by a polynomial for large values of n of degree at most d-1. It is of some interest to find the degree of this polynomial. We show that when the degree of this polynomial is less than d-1 then the fiber module F(I,M) is free over the fiber cone F(I).
I will also talk about some results on graded local cohomology modules and a generalization of Grothendieck-Serre difference formula.