Date & Time: Monday, August 24, 2009, 15:30-17:00.
Venue: Room 215
Title: Injective Hulls Matlis Duality - I
Speaker: Shreedevi Masuti, IIT Bombay
Abstract: Any module M can be embedded into an injective module E. Such an embedding can be chosen to be minimal. In this case, E is uniquely determined and it is called the injective hull of M. Over a Noetherian ring R, any module can be decomposed uniquely as a direct sum of indecomposable injective modules. Indecomposable injective modules turn out to be injective hulls of R/P where P is some prime ideal of R. If R is local with maximal ideal 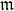 and E is the injective hull of R/
and E is the injective hull of R/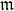 , then the functor Hom(-, E) establishes an anti-equivalence between the category of Artininan R-modules and the category of finite R-modules. This is known as Matlis duality which plays a fundamental role in the study of Gorenstein rings.
, then the functor Hom(-, E) establishes an anti-equivalence between the category of Artininan R-modules and the category of finite R-modules. This is known as Matlis duality which plays a fundamental role in the study of Gorenstein rings.